排序算法

算法一：冒泡排序

对于基本的冒泡排序思路：遍历一个集合，对比相近的两个元素，大的置后 ---> 效果是：将本次循环中最大的元素置于本次循环的最后

可能，在本次循环中后面几个已经是有序的且最大，但是并不关心(下次循环仍然要遍历到)

"""
列表的长度n
j代表外层循环的下标， i为内层循环遍历的下标
j的遍历次数：n-1
j=0 i:0 ~ n-1
j=1 i:0 ~ n-2
j与i的关系：i = n-1-j
"""

def bubble_sort(alist):
    for j in range(len(alist) - 1):
        for i in range(len(alist) - 1 - j):
            if alist[i] > alist[i + 1]:
                alist[i], alist[i + 1] = alist[i + 1], alist[i]

或者

def bubble_sort2(alist):
    for j in range(len(alist) - 1, 0, -1):
        for i in range(j):
            if alist[i] > alist[i + 1]:
                alist[i], alist[i + 1] = alist[i + 1], alist[i]

# 最优时间复杂度和最坏时间复杂度都是O(n^2)
# 稳定性：稳定

如果本次循环中没有进行过元素交换，就可以认为本次循环已经完成了排序 ---> 设置变量进行判断

def bubble_sort3(alist):
    for j in range(len(alist) - 1):
        ctn = 0
        for i in range(len(alist) - 1 - j):
            if alist[i] > alist[i + 1]:
                alist[i], alist[i + 1] = alist[i + 1], alist[i]
                ctn += 1
        # 如果在那次遍历的时候没有任何交换，则说明原本就是有序的
        if ctn == 0: break

# 最优时间复杂度 O(n)
# 最坏时间复杂度 O(n^2)

上诉两种都是将最大的数字后置，下次循环避免(只关心本次循环最大的数字是谁)，但是有些区域本来就是符合最终排序效果

# 双向冒泡(鸡尾酒排序)
def bubble_sort4(alist):
    # 左右指针的位置，代表循环遍历的范围
    left, right = 0, len(alist) - 1
    # 当左右指针不重合时循环
    while left < right:
        swap_point = left  # 假设最后一次交换点位置
        for i in range(left, right):
            if alist[i] > alist[i + 1]:
                alist[i], alist[i + 1] = alist[i + 1], alist[i]
                swap_point = i
        # 右侧最后一次交换区，此交换区后的皆为有序，且最大
        right = swap_point
        # 反向冒泡,最后一次交换区之前的皆为有序，且最小
        for i in range(right, left, -1):
            if alist[i] < alist[i - 1]:
                alist[i], alist[i - 1] = alist[i - 1], alist[i]
                swap_point = i
        left = swap_point

算法二：选择排序

思路是将一个集合分为两个部分对待，不断选出后半部分的最小值往前半部分插

# 代码实现
def select_sort(ls):
    n = len(ls)
    for j in range(n - 1):
        min_val = j
        for i in range(j + 1, n):
            if ls[min_val] > ls[i]:
                min_val = i
        ls[j], ls[min_val] = ls[min_val], ls[j]

if __name__ == '__main__':
    ll = [1, 4, 2, 6, 8, 7, 11, 34]
    res = select_sort(ll)
    print(res)

# 最优时间复杂度：O(n^2);最坏时间复杂度：O(n^2)
# 稳定度：不稳定(考虑升序，选择最大值，往后插入的情况)

算法三：插入排序

插入排序将序列分为有序区和无序区两个部分，最初有序区只有一个元素，每次从无序区选择一个元素，插入到有序区的合理位置，直到无序区变空

def insert_sort2(ls):
    n = len(ls)
    for j in range(1, n):
        for i in range(j, 0, -1):
            if ls[i] < ls[i - 1]:
                ls[i], ls[i - 1] = ls[i - 1], ls[i]
            else:
                break

def insert_sort(ls):
    n = len(ls)
    for j in range(1, n):
        i = j
        while i > 0:
            if ls[i] < ls[i - 1]:
                ls[i], ls[i - 1] = ls[i - 1], ls[i]
                i -= 1
            else:
                break

if __name__ == '__main__':
    ls = [1, 9, 8, 4, 2, 12, 23, 42, 24]
    # insert_sort(ls)
    insert_sort2(ls)
    print(ls)

# 最优时间复杂度：O(n),最坏时间复杂度：O(n^2)
# 稳定性：稳定

算法四：快速排序

快速排序的实现方法是：假如有一个列表ls=[12,3,6,7,4,5,9]

整体思路：将列表的第一个元素作为目标元素，用两个指针low(该指针实现的效果：左边的数字应该比目标小)及high(该指针实现的效果：右边的数字应该比目标大)遍历列表，将目标元素放到合适的位置上，然后以该元素为点，拆分列表重复上述操作

具体思路：用一个变量记录目标元素(该位置的元素可视为空)，low指针在列表的头，high在尾，让high指针移动，如果high所指元素大于目标元素，则high指针继续向左移动，如果小于，将该元素置于low指针所指位置(此时high所指的位置，可视为空)，然后让low移动，如果low指针所指的元素小于目标元素，则low指针向右移动，反之，将该元素置于high指针所指位置，然后再移动high指针，直至两指针重合，然后以目标元素位置为点，将列表拆分为左右两部分再进行遍历，值得注意的是这种拆分只是形式上的，操作排序仍然在原列表上，不会生成新的列表

代码实现

def quick_sort(ls, first, last):
    # 递归结束条件
    if first >= last:
        return
    mid_val = ls[first]
    low = first
    high = last
    # 该循环控制两指针之间的切换
    while low < high:
        # 该循环控制单个指针的移动
        while low < high and ls[high] >= mid_val:
            high -= 1
        ls[low] = ls[high]
        while low < high and ls[low] <= mid_val:
            low += 1
        ls[high] = ls[low]
    # 将目标元素置于合适位置
    ls[low] = mid_val
    # 目标元素左半部分
    quick_sort(ls, first, low - 1)
    # 目标元素右半部分
    quick_sort(ls, low + 1, last)


if __name__ == '__main__':
    ls = [12, 3, 5, 4, 31, 9, 6]
    quick_sort(ls, 0, len(ls)-1)
    print(ls)

# 最优时间复杂度：n*log2n；最坏时间复杂度：n^2
# 稳定性：不稳定

算法五：归并排序

归并排序的思想是分解与归并

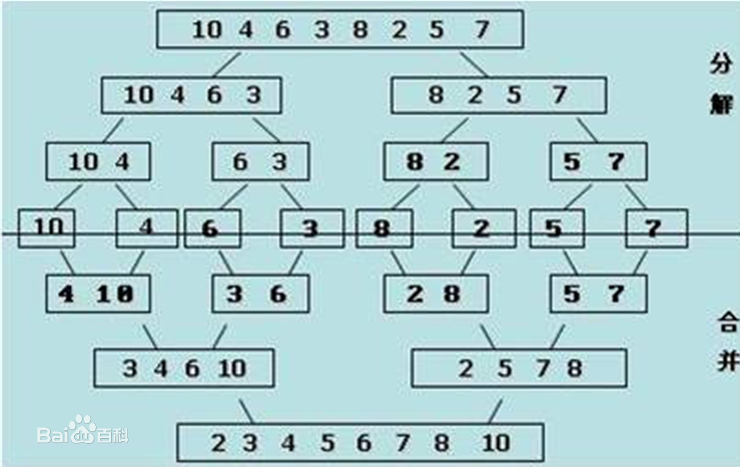
def merge(li, left, mid, right):
    i = left
    j = mid + 1
    ltmp = []
    while i <= mid and j <= right:
        if li[i] < li[j]:
            ltmp.append(li[i])
            i += 1
        else:
            ltmp.append(li[j])
            j += 1
    while i <= mid:
        ltmp.append(li[i])
        i += 1

    while j <= right:
        ltmp.append(li[j])
        j += 1

    li[left:right+1] = ltmp

def merge_sort(li, left, right):

    if left < right:
        mid = (left + right) // 2
        merge_sort(li, left, mid)
        merge_sort(li, mid+1, right)
        print('归并之前:', li[left:right+1])
        merge(li, left, mid, right)
        print('归并之后:', li[left:right+1])

li = [10,4,6,3,8,2,5,7]
merge_sort(li, 0, len(li)-1)

# 时间复杂度: O(nlogn)
# 空间复杂度: O(n)

算法六：希尔排序

是一种分组插入排序，首先取一个整数d = n/2,将元素分为d个组，每组每组相邻元素之间距离为d,在各组内进行插入排序，

取第二个整数d2 = d/2,重复上述过程，直到dn = 1,

希尔排序每趟并不使某些元素有序，而是使整体数据越来越接近有序，最后一趟排序使得所有数据有序

def shell_sort(ls):
    n = len(ls)
    gep = n // 2
    while gep > 0:
        for j in range(gep, n):
            i  = j
            while i > 0:
                if ls[i] < ls[i - gep]:
                    ls[i], ls[i - gep] = ls[i - gep], ls[i]
                    i -= gep
                else:
                    break
        gep //= 2


if __name__ == '__main__':
　　ls = [1, 9, 8, 4, 2, 12, 23, 42, 24]
　　shell_sort(ls)
　　print(ls)


最优时间复杂度：随gep的取值改变，最坏时间复杂度：O(n^2)
稳定性：不稳定

算法七：计数排序

计数排序的思想是

假设现在有一个列表ls，我们创建另一个列表L用来计数。即，L列表每个下标对应ls列表中的值，比如：ls有一个4，那么我们为L列表索引为4的值加1：L[4] +=1。代表，4出现过一次。此外，L的长度应该为ls列表最大值加1，初识值为0

代码实现

def count_sort(ls, max_num):
    count = [0 for i in range(max_num + 1)]
    for num in ls:
        count[num] += 1
    i = 0
    for num, m in enumerate(count):
        for j in range(m):
            ls[i] = num
            i += 1




ls = [1,10,7,4,2,3,5,6]
count_sort(ls,10)
print(ls)

性能测试

def run_time(func):
    def inner(*args,**kwargs):
        start = time.time()
        func(*args,**kwargs)
        end =time.time()
        print(end - start)
    return inner

除了使用装饰器计数代码运行时间外，还可以使用内置的timeit模块

from timeit import Timer


def t1():
    L = []
    for i in range(100):
        L.append(i)


def t2():
    L = []
    for i in range(100):
        L.insert(0, i)


timer_obj1 = Timer("t1()", "from __main__ import t1")
print("1", timer_obj1.timeit())


timer_obj2 = Timer("t2()", "from __main__ import t2")
print("2", timer_obj2.timeit())

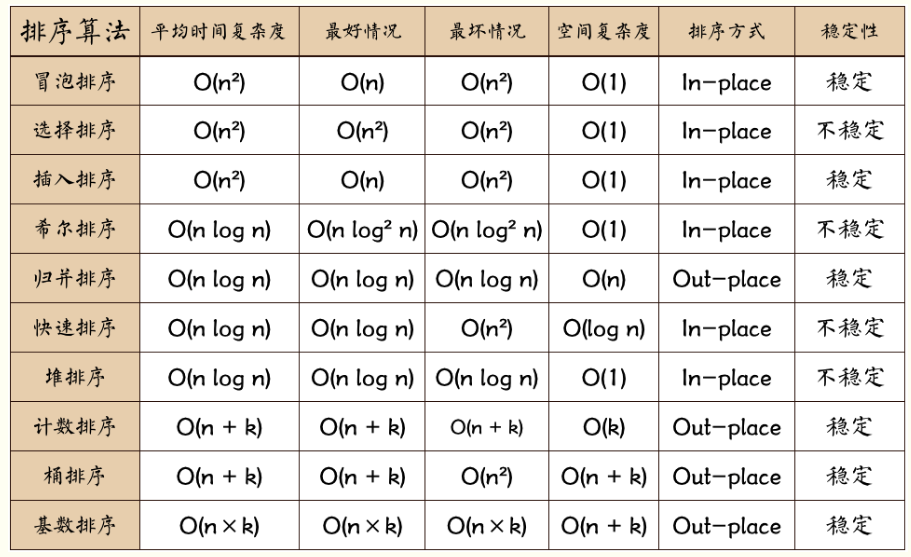
排序小结：